哈希

1. 两数之和

给定一个整数数组 nums 和一个整数目标值 target，请你在该数组中找出 和为目标值 *target*  的那 两个 整数，并返回它们的数组下标。

你可以假设每种输入只会对应一个答案，并且你不能使用两次相同的元素。

你可以按任意顺序返回答案。

提示：

2 <= nums.length <= 104

109 <= nums[i] <= 109

109 <= target <= 109

只会存在一个有效答案

示例：

1
2
3
4
5
6
7
输入：nums = [2,7,11,15], target = 9
输出：[0,1]
解释：因为 nums[0] + nums[1] == 9 ，返回 [0, 1] 

输入：nums = [3,2,4], target = 6
输出：[1,2]
解释：因为 nums[1] + nums[2] == 6 , 返回[1, 2]

代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
/**
     * **进阶**：**时间复杂度小于 O(n2) 的算法解决此问题吗？**
     * 1. 使用一个哈希表存储数组元素及其下标。
     * 2. 遍历数组，对于每个元素，检查哈希表中是否存在目标值减去当前元素的值。
     * 3. 如果存在，返回这两个元素的下标；否则，将当前元素及其下标存入哈希表。
     * 4. 如果遍历结束未找到，返回默认值 [0, 0]。
     * @param nums   给定一个整数数组
     * @param target 整数目标值
     * @return 数组下标
     */
    public int[] twoSum(int[] nums, int target) {
        Map<Integer, Integer> map = new HashMap<>();
        for (int i = 0; i < nums.length; i++) {
            int num = nums[i];
            if (map.containsKey(target - num)) {
                return new int[] {map.get(target - num), i};
            }
            map.put(num, i);
        }
        return new int[] {0,0};
    }

2. 字母异位词分组

给你一个字符串数组，请你将 字母异位词 组合在一起。可以按任意顺序返回结果列表。

字母异位词 是由重新排列源单词的所有字母得到的一个新单词。

提示：

1 <= strs.length <= 104

0 <= strs[i].length <= 100

strs[i] 仅包含小写字母

提示：

1
2
3
4
5
6
7
8
输入: strs = ["eat", "tea", "tan", "ate", "nat", "bat"]
输出: [["bat"],["nat","tan"],["ate","eat","tea"]]

输入: strs = [""]
输出: [[""]]

输入: strs = ["a"]
输出: [["a"]]

代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
/**
  * 将一组字符串按照字母异位词分组
  * 字母异位词指的是字符组成相同，但排列顺序不同的字符串
  *
  * @param strs 待分组的字符串数组
  * @return 分组后的字母异位词列表，每个元素都是一个字符串列表，包含互为字母异位词的字符串
  */
 public List<List<String>> groupAnagrams(String[] strs) {
     // 使用哈希表存储分组结果，键为排序后的字符串哈希值，值为字符串列表
     Map<Integer, List<String>> map = new HashMap<>();
     for (String str : strs) {
         // 将字符串转换为字符数组，便于排序
         char[] chars = str.toCharArray();
         // 对字符数组进行排序，使得字母异位词拥有相同的键值
         Arrays.sort(chars);
         // 使用排序后的字符串作为键值，获取其哈希码
         int key = new String(chars).hashCode();
         // 从哈希表中获取与计算出的键值相关联的字符串列表，如果不存在则创建一个新的列表
         List<String> orDefault = map.getOrDefault(key, new ArrayList<>());
         // 如果当前键值对应的列表为空，则将其放入哈希表中
         if (orDefault.isEmpty()) {
             map.put(key, orDefault);
         }
         // 将当前字符串添加到对应键值的列表中
         orDefault.add(str);
     }
     // 返回分组后的字母异位词列表，转换为ArrayList以满足返回类型要求
     return new ArrayList<>(map.values());
 }
 
 /**
  由于互为字母异位词的两个字符串包含的字母相同，因此两个字符串中的相同字母出现的次数
  一定是相同的，故可以将每个字母出现的次数使用字符串表示，作为哈希表的键。
  由于字符串只包含小写字母，因此对于每个字符串，可以使用长度为26的数组
  记录每个字母出现的次数。需要注意的是，在使用数组作为哈希表的键时，不同语言的支持程度不同，因此不同语言的实现方式也不同
 */
 public List<List<String>> groupAnagrams(String[] strs) {
     Map<String, List<String>> map = new HashMap<String, List<String>>();
     for (String str : strs) {
         int[] counts = new int[26];
         int length = str.length();
         for (int i = 0; i < length; i++) {
             counts[str.charAt(i) - 'a']++;
         }
         // 将每个出现次数大于 0 的字母和出现次数按顺序拼接成字符串，作为哈希表的键
         StringBuffer sb = new StringBuffer();
         for (int i = 0; i < 26; i++) {
             if (counts[i] != 0) {
                 sb.append((char) ('a' + i));
                 sb.append(counts[i]);
             }
         }
         String key = sb.toString();
         List<String> list = map.getOrDefault(key, new ArrayList<String>());
         list.add(str);
         map.put(key, list);
     }
     return new ArrayList<List<String>>(map.values());
 }

3. 最长连续序列

给定一个未排序的整数数组 nums ，找出数字连续的最长序列（不要求序列元素在原数组中连续）的长度。

请你设计并实现时间复杂度为 O(n) **的算法解决此问题

提示：

0 <= nums.length <= 105

109 <= nums[i] <= 109

示例：

1
2
3
4
5
6
7
8
9
输入：nums = [100,4,200,1,3,2]
输出：4
解释：最长数字连续序列是 [1, 2, 3, 4]。它的长度为 4。

输入：nums = [0,3,7,2,5,8,4,6,0,1]
输出：9

输入：nums = [1,0,1,2]
输出：3

代码：

1
2
3
4
5
6
7
8
9
10
11
public int longestConsecutive(int[] nums) {
    Arrays.sort(nums);
    Map<Integer, Integer> map = new HashMap<>();
    int r = 0;
    for (int num : nums) {
        int i1 = map.getOrDefault(num - 1, 0) + 1;
        r = Math.max(r, i1);
        map.put(num, i1);
    }
    return r;
}

位运算

1. 奇偶位数

给你一个 正 整数 n 。

用 even 表示在 n 的二进制形式（下标从 0 开始）中值为 1 的偶数下标的个数。

用 odd 表示在 n 的二进制形式（下标从 0 开始）中值为 1 的奇数下标的个数。

请注意，在数字的二进制表示中，位下标的顺序 从右到左。

返回整数数组 **answer **，其中 **answer = [even, odd]

提示：

1 <= n <= 1000

示例：

1
2
3
4
5
6
7
8
9
10
11
输入：n = 50
输出：[1,2]
解释：
50 的二进制表示是 110010。
在下标 1，4，5 对应的值为 1。

输入：n = 2
输出：[0,1]
解释：
2 的二进制表示是 10。
只有下标 1 对应的值为 1。

代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
/**
 * 用i=0表示当前位是奇数位，i=1表示当前位是偶数位，并记录对应奇偶数位的结果。
 * 当n>0时，如果当前位是1，则增加对应奇偶位的计数，然后反转i并将n作右移位运算。
 * 循环以上过程，直到n=0，最后返回结果。
 * @param n 输入的整数
 * @return 结果数组
 */
public int[] evenOddBit(int n) {
    int[] res = new int[2];
    int i = 0;
    while (n > 0) {
        res[i] += n & 1;
        n >>= 1;
        i ^= 1;
    }
    return res;
}

双指针

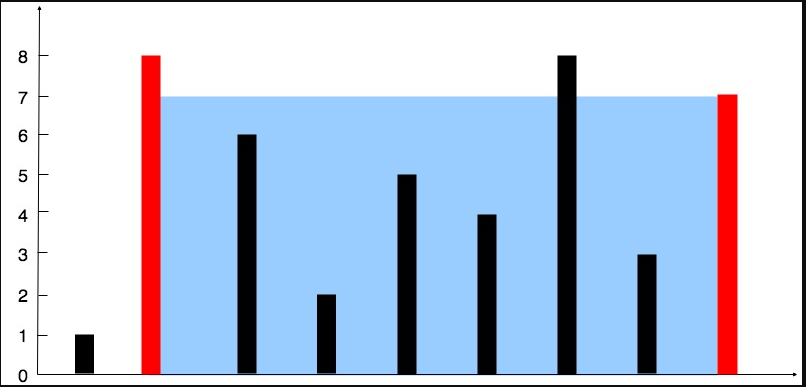
1. 移动零

给定一个数组 nums，编写一个函数将所有 0 移动到数组的末尾，同时保持非零元素的相对顺序（原数组的顺序）。

请注意 ，必须在不复制数组的情况下原地对数组进行操作。

**进阶：**你能尽量减少完成的操作次数吗？

提示：

1 <= nums.length <= 104

231 <= nums[i] <= 231 - 1

示例：

1
2
3
4
5
输入: nums = [0,1,0,3,12]
输出: [1,3,12,0,0]

输入: nums = [0]
输出: [0]

代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
/**
   * 我们创建两个指针i和j，第一次遍历的时候指针j用来记录当前有多少非0元素。 
   * 即遍历的时候每遇到一个非0元素就将其往数组左边挪，第一次遍历完后，j指针的下标就指向了最后一个非0元素下标。
   * 第二次遍历的时候，起始位置就从j开始到结束，将剩下的这段区域内的元素全部置为
   *
   * @param nums x 
  */
 public void moveZeroes(int[] nums) {
      if (nums == null) {
          return;
      }
      //第一次遍历的时候，j指针记录非0的个数，只要是非0的统统都赋给nums[j]
      int j = 0;
      for (int i = 0; i < nums.length; ++i) {
          if (nums[i] != 0) {
              nums[j++] = nums[i];
          }
      }
      //非0元素统计完了，剩下的都是0了
      //所以第二次遍历把末尾的元素都赋为0即可
      for (int i = j; i < nums.length; ++i) {
          nums[i] = 0;
      }
  }
	

 /**
   * 这里参考了快速排序的思想，快速排序首先要确定一个待分割的元素做中间点x，然后把所有小于等于x的元素放到x的左边，大于x的元素放到其右边。
   * 这里我们可以用0当做这个中间点，把不等于0(注意题目没说不能有负数)的放到中间点的左边，等于0的放到其右边。
   * 这的中间点就是0本身，所以实现起来比快速排序简单很多，我们使用两个指针i和j，只要nums[i]!=0，我们就交换nums[i]和nums[j]
   * 请对照动态图来理解
   *
   * @param nums x
   */
 public void moveZeroes(int[] nums) {
      int l, r = 0;
      for (l = 0; l < nums.length; l++) {
          if (nums[l] != 0) {
              swap(nums, l, r);
              r++;
          }
      }
  }
  
  
  public void swap(int[] nums, int l, int r) {
      int temp = nums[l];
      nums[l] = nums[r];  
      nums[r] = temp;
  }

2. 盛最多水的容器

给定一个长度为 n 的整数数组 height 。有 n 条垂线，第 i 条线的两个端点是 (i, 0) 和 (i, height[i]) 。

找出其中的两条线，使得它们与 x 轴共同构成的容器可以容纳最多的水。

返回容器可以储存的最大水量。

**说明：**你不能倾斜容器。

提示：

n == height.length

2 <= n <= 105

0 <= height[i] <= 104

示例：

image.png

1
2
3
4
5
6
7
输入：[1,8,6,2,5,4,8,3,7]
输出：49 
解释：图中垂直线代表输入数组 [1,8,6,2,5,4,8,3,7]。在此情况下，
容器能够容纳水（表示为蓝色部分）的最大值为 49。

输入：height = [1,1]
输出：1

代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
/**
  * @param height 高度
  * @return 面积
  * <p>
  * 暴力法：
  * 遍历数组，计算每个位置的左右指针之间的面积，并更新最大面积。
  * <p>
  * 优化：
  * 双指针法：
  * 初始化左右指针，计算初始面积。
  * 移动指针：
  * 如果左指针的高度小于右指针的高度，则将左指针向右移动，并更新面积。
  * 如果左指针的高度大于右指针的高度，则将右指针向左移动，并更新面积。
  *循环直到左指针大于右指针。
  */
 public int maxArea(int[] height) {
     int max = 0, l = 0, r = height.length - 1;
     while (l < r) {
         int area = Math.min(height[l], height[r]) * (r - l);
         max = Math.max(max, area);
         if (height[l] < height[r]) {
             l++;
         } else {
             r--;
         }
     }
     return max;
 }

3. 三数之和

给你一个整数数组 nums ，判断是否存在三元组 [nums[i], nums[j], nums[k]] 满足 i != j、i != k 且 j != k ，同时还满足 nums[i] + nums[j] + nums[k] == 0 。请你返回所有和为 0 且不重复的三元组。

**注意：**答案中不可以包含重复的三元组。

提示：

3 <= nums.length <= 3000

105 <= nums[i] <= 105

示例：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
输入：nums = [-1,0,1,2,-1,-4]
输出：[[-1,-1,2],[-1,0,1]]
解释：
nums[0] + nums[1] + nums[2] = (-1) + 0 + 1 = 0 。
nums[1] + nums[2] + nums[4] = 0 + 1 + (-1) = 0 。
nums[0] + nums[3] + nums[4] = (-1) + 2 + (-1) = 0 。
不同的三元组是 [-1,0,1] 和 [-1,-1,2] 。
注意，输出的顺序和三元组的顺序并不重要。

输入：nums = [0,1,1]
输出：[]
解释：唯一可能的三元组和不为 0 。
输入：nums = [0,0,0]
输出：[[0,0,0]]
解释：唯一可能的三元组和为 0 。

代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
/**
 * <p>三数之和</p>
 * 排序处理 + 双指针   
 *
 * @param nums 数组
 * @return 三元组
 */
public List<List<Integer>> threeSum(int[] nums) {
    Arrays.sort(nums);
    Map<String, List<Integer>>  map = new HashMap<>();
    int l, r, k = nums.length - 1;
    while (k > 1) {
        r = k - 1;
        l = 0;
        while (l < r) {
            int i = nums[l] + nums[r] + nums[k];
            if (i == 0) {
                String key = String.valueOf(nums[l]) + nums[r] + nums[k];
                if (!map.containsKey(key)) {
                    map.put(key, Arrays.asList(nums[l], nums[r], nums[k]));
                }
                r--;
                l++;
            } else if (i > 0) {
                r--;
            } else {
                l++;
            }
        }
        k--;
    }
    return new ArrayList<>(map.values());
}

/**
 * 优化 去除重复元素
 * 寻找数组中所有不重复的三元组，这些三元组的和为零
 *
 * @param nums 输入的整数数组
 * @return 返回一个列表，包含所有和为零的不重复三元组
 */
public List<List<Integer>> threeSum(int[] nums) {
    // 先排序
    Arrays.sort(nums);
    List<List<Integer>> res = new ArrayList<>();

    for (int i = 0; i < nums.length; i++) {
        // 跳过重复元素
        if (i > 0 && nums[i] == nums[i - 1]) {
            continue;
        }

        // 双指针，目标是找到 nums[l] + nums[r] = -nums[i]
        int l = i + 1, r = nums.length - 1;
        int target = -nums[i];

        while (l < r) {
            int sum = nums[l] + nums[r];
            if (sum == target) {
                res.add(Arrays.asList(nums[i], nums[l], nums[r]));
                l++;
                r--;
                // 跳过重复元素
                while (l < r && nums[l] == nums[l - 1]) {
                    l++;
                }
                while (l < r && nums[r] == nums[r + 1]) {
                    r--;
                }
            } else if (sum < target) {
                l++;
            } else {
                r--;
            }
        }
    }

    return res;
}

4. 接雨水

给定 n 个非负整数表示每个宽度为 1 的柱子的高度图，计算按此排列的柱子，下雨之后能接多少雨水。
提示：

n == height.length

1 <= n <= 2 * 104

0 <= height[i] <= 105

示例：

image.png

1
2
3
4
5
6
输入：height = [0,1,0,2,1,0,1,3,2,1,2,1]
输出：6
解释：上面是由数组 [0,1,0,2,1,0,1,3,2,1,2,1] 表示的高度图，在这种情况下，可以接 6 个单位的雨水（蓝色部分表示雨水）。

输入：height = [4,2,0,3,2,5]
输出：9

代码：解法

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
public int trap(int[] height) {
    int n = height.length;
    int res = 0;
    // 左右指针：分别指向左右两边界的列
    int left = 0, right = n - 1;
    // 左指针的左边最大高度、右指针的右边最大高度
    int leftMax = height[left], rightMax = height[right];
    // 最两边的列存不了水
    left++;
    right--;
    // 向中间靠拢
    while(left <= right){
        leftMax = Math.max(leftMax, height[left]);
        rightMax = Math.max(rightMax, height[right]);
        if(leftMax < rightMax){
            // 左指针的leftMax比右指针的rightMax矮
            // 说明：左指针的右边至少有一个板子 > 左指针左边所有板子
            // 根据水桶效应，保证了左指针当前列的水量决定权在左边
            // 那么可以计算左指针当前列的水量：左边最大高度-当前列高度
            res += leftMax - height[left];
            left++;
        }else{
            // 右边同理
            res += rightMax - height[right];
            right--;
        }
    }
    return res;
}

滑动窗口

1. 无重复字符的最长子串

给定一个字符串 s ，请你找出其中不含有重复字符的 最长 子串 的长度。

提示：

0 <= s.length <= 5 * 104

s 由英文字母、数字、符号和空格组成

示例：

1
2
3
4
5
6
7
8
9
10
11
12
输入: s = "abcabcbb"
输出: 3 
解释: 因为无重复字符的最长子串是 "abc"，所以其长度为 3。

输入: s = "bbbbb"
输出: 1
解释: 因为无重复字符的最长子串是 "b"，所以其长度为 1。

输入: s = "pwwkew"
输出: 3
解释: 因为无重复字符的最长子串是 "wke"，所以其长度为 3。
     请注意，你的答案必须是 子串 的长度，"pwke" 是一个子序列，不是子串。

代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
/**
 * 计算字符串中最长无重复字符的子串的长度
 * 通过维护一个滑动窗口，使用HashSet来记录窗口中的字符，确保无重复
 * 当遇到重复字符时，移动窗口的左边界，直到移除该重复字符
 * 在每次迭代中更新最长无重复子串的长度
 *
 * @param s 输入的字符串
 * @return 最长无重复字符的子串的长度
 */
public int lengthOfLongestSubstring(String s) {
    // 将字符串转换为字符数组，便于逐个字符处理
    char[] charArray = s.toCharArray();
    // 初始化最长无重复子串的长度为0
    int res = 0;
    // 使用HashSet存储当前遍历的无重复字符
    Set<Character> set = new HashSet<>();
    // 初始化滑动窗口的左右指针i和j，从字符串的开始位置出发
    for (int i = 0, j = 0; j < charArray.length; j++) {
        // 获取当前遍历的字符
        char c = charArray[j];
        // 当字符已经存在于Set中时，循环移除字符，直到移除重复的字符
        while (set.contains(c)) {
            set.remove(charArray[i]);
            i++;
        }
        // 将当前字符添加到Set中
        set.add(c);
        // 更新最长无重复子串的长度
        res = Math.max(res, j - i + 1);
    }
    // 返回最长无重复子串的长度
    return res;
}

2. 找到字符串中所有字母异位词

给定两个字符串 s 和 p，找到 s ****中所有 p ****的 异位词 的子串，返回这些子串的起始索引。不考虑答案输出的顺序。
提示：

1 <= s.length, p.length <= 3 * 104

s 和 p 仅包含小写字母

示例：

1
2
3
4
5
6
7
8
9
10
11
12
输入: s = "cbaebabacd", p = "abc"
输出: [0,6]
解释:
起始索引等于 0 的子串是 "cba", 它是 "abc" 的异位词。
起始索引等于 6 的子串是 "bac", 它是 "abc" 的异位词。

输入: s = "abab", p = "ab"
输出: [0,1,2]
解释:
起始索引等于 0 的子串是 "ab", 它是 "ab" 的异位词。
起始索引等于 1 的子串是 "ba", 它是 "ab" 的异位词。
起始索引等于 2 的子串是 "ab", 它是 "ab" 的异位词。

代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
public List<Integer> findAnagrams(String s, String p) {
    List<Integer> ans = new ArrayList<Integer>();
    int slen = s.length();
    int plen = p.length();

    // 判不合理
    if(slen<plen){
        return new ArrayList<Integer>();
    }

    int[] count = new int[26];
    // 用起始索引0的情况初始化count数组
    for(int i=0;i<plen;i++){
        count[s.charAt(i)-'a']++;
        count[p.charAt(i)-'a']--;
    }

    // 初始化differ
    int differ=0;
    for(int j=0;j<26;j++){
        if(count[j]!=0){
            differ++;
        }
    }
    // 初始化ans
    if(differ==0){
        ans.add(0);
    }
    // 滑动过程，起始索引是i+1
    for(int i=0;i<slen-plen;i++){
        // 把左端滑出窗口，判断differ变化
        count[s.charAt(i)-'a']--;
        if(count[s.charAt(i)-'a']==0){
            differ--;
        }else if(count[s.charAt(i)-'a']==-1){
            differ++;
        }
        // 把右端滑入，判断differ变化
        count[s.charAt(i+plen)-'a']++;
        if(count[s.charAt(i+plen)-'a']==0){
            differ--;
        }
        else if(count[s.charAt(i+plen)-'a']==1){
            differ++;
        }
        
        // 符合条件否
        if(differ==0){
            ans.add(i+1);
        }
    }
    return ans;
}

子串

1. 和为 K 的子数组

给你一个整数数组 nums 和一个整数 k ，请你统计并返回 *该数组中和为 k ***的子数组的个数 。

子数组是数组中元素的连续非空序列。

提示：

1 <= nums.length <= 2 * 104

1000 <= nums[i] <= 1000

107 <= k <= 107

示例：

1
2
3
4
5
输入：nums = [1,1,1], k = 2
输出：2

输入：nums = [1,2,3], k = 3
输出：2

代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
public int subarraySum(int[] nums, int k) {
    /*用哈希表的前缀和做法*/
    /* 这里相当于利用哈希表存储了当前数之前的前缀和有无等于A-k的，
    因为比如说对于[1,1,1]，它的前缀和数组为[0,1,2,3],对于索引为2的前缀和
    数组处即2(它此时就是A=2的)，假设k=1，就是判断[0,1]处有无等于A-k的，这里
    是有一个的 */
    /* 有点像两数之和，不过那个是在整个哈希表中找k-A的 */
    Map<Integer,Integer> map=new HashMap<>();
    int count=0;
    /* 为什么map key为0赋值为1，比如对于上个例子，前缀和索引为1处此时A-k就等于0
    它在map中是已经存在的，此时count要++，故赋值为1 */
    map.put(0,1);
    int pre_sum=0;
    for(int i=0;i<nums.length;++i){
        /* 点睛之笔，在当前前缀和之前的map中找 */
        pre_sum+=nums[i];
        if(map.containsKey(pre_sum-k)){
            count+=map.get(pre_sum-k);
        }
        map.put(pre_sum,map.getOrDefault(pre_sum,0)+1);
    }
    return count;
}

2. 滑动窗口最大值

给你一个整数数组 nums，有一个大小为 k **的滑动窗口从数组的最左侧移动到数组的最右侧。你只可以看到在滑动窗口内的 k 个数字。滑动窗口每次只向右移动一位。

返回 滑动窗口中的最大值 。

提示：

1 <= nums.length <= 105

104 <= nums[i] <= 104

1 <= k <= nums.length

示例：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
输入：nums = [1,3,-1,-3,5,3,6,7], k = 3
输出：[3,3,5,5,6,7]
解释：
滑动窗口的位置                最大值
---------------               -----
[1  3  -1] -3  5  3  6  7       3
 1 [3  -1  -3] 5  3  6  7       3
 1  3 [-1  -3  5] 3  6  7       5
 1  3  -1 [-3  5  3] 6  7       5
 1  3  -1  -3 [5  3  6] 7       6
 1  3  -1  -3  5 [3  6  7]      7
 
输入：nums = [1], k = 1
输出：[1]

代码：

解法说明

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
/**
 * 计算滑动窗口中的最大值
 * 本方法通过维护前缀和后缀最大值数组来高效计算每个滑动窗口的最大值
 * 1. 优先队列算法
 * 2. 单调队列算法
 * 3. 分块 + 预处理
 *
 * @param nums 输入的整数数组
 * @param k 滑动窗口的大小
 * @return 每个滑动窗口的最大值组成的数组
 */
public int[] maxSlidingWindow(int[] nums, int k) {
    int n = nums.length;
    
    // suffixMax数组用于存储从每个位置开始向后k个元素中的最大值
    int[] suffixMax = new int[n];
    // prefixMax数组用于存储到每个位置结束向前k个元素中的最大值
    int[] prefixMax = new int[n];
    
    // 计算suffixMax数组
    for (int i = 0; i < n; i++) {
        if (i % k == 0) {
            suffixMax[i] = nums[i];
        } else {
            suffixMax[i] = Math.max(suffixMax[i - 1], nums[i]);
        }
    }
    
    // 计算prefixMax数组
    for (int i = n - 1; i >= 0; i--) {
        if (i == n - 1 || (i + k) % k == 0) {
            prefixMax[i] = nums[i];
        } else {
            prefixMax[i] = Math.max(prefixMax[i + 1], nums[i]);
        }
    }
    
    // ans数组用于存储每个滑动窗口的最大值
    int[] ans = new int[n - k + 1];
    for (int i = 0; i < n - k + 1; i++) {
        // 每个滑动窗口的最大值是其suffixMax和prefixMax中的较大者
        ans[i] = Math.max(suffixMax[i + k - 1], prefixMax[i]);
    }
    
    return ans;
}

3. 最小覆盖子串

给你一个字符串 s 、一个字符串 t 。返回 s 中涵盖 t 所有字符的最小子串。如果 s 中不存在涵盖 t 所有字符的子串，则返回空字符串 "" 。

**进阶：**你能设计一个在 o(m+n) 时间内解决此问题的算法吗？

注意：

  • 对于 t 中重复字符，我们寻找的子字符串中该字符数量必须不少于 t 中该字符数量。
  • 如果 s 中存在这样的子串，我们保证它是唯一的答案。

提示：

m == s.length

n == t.length

1 <= m, n <= 105

s 和 t 由英文字母组成

示例：

1
2
3
4
5
6
7
8
9
10
11
12
输入：s = "ADOBECODEBANC", t = "ABC"
输出："BANC"
解释：最小覆盖子串 "BANC" 包含来自字符串 t 的 'A'、'B' 和 'C'。

输入：s = "a", t = "a"
输出："a"
解释：整个字符串 s 是最小覆盖子串。

输入: s = "a", t = "aa"
输出: ""
解释: t 中两个字符 'a' 均应包含在 s 的子串中，
因此没有符合条件的子字符串，返回空字符串。

代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
public String minWindow(String s, String t) {

    int[] map = new int[58];
    for (char c : t.toCharArray()) {
        map[c - 'A']++;
    }
    // 窗口左右指针
    int left = 0, right = 0;
    // 最小窗口长度
    int minLen = Integer.MAX_VALUE;
    // 窗口起始位置
    int minLeft = 0; 
    // 需要匹配的字符总数
    int count = t.length(); 

    while (right < s.length()) {
        char c = s.charAt(right);
        // 当前字符在t中存在，减少计数
        if (map[c - 'A'] > 0) {
            count--;
        }
        map[c - 'A']--; // 不论是否在t中，都减少计数（负数表示窗口中的冗余字符）

        // 当窗口包含所有t的字符时，尝试收缩左边界
        while (count == 0) {
            // 更新最小窗口
            if (right - left + 1 < minLen) {
                minLen = right - left + 1;
                minLeft = left;
            }

            // 左边界右移，恢复字符计数
            char leftChar = s.charAt(left);
            map[leftChar - 'A']++;
            // 如果恢复后该字符的计数大于0，说明移除了一个必需的字符，需增加count
            if (map[leftChar - 'A'] > 0) {
                count++;
            }
            left++;
        }
        right++;
    }

    return minLen == Integer.MAX_VALUE ? "" : s.substring(minLeft, minLeft + minLen);
}

普通数组

1. 最大子数组和

给你一个整数数组 nums ，请你找出一个具有最大和的连续子数组（子数组最少包含一个元素），返回其最大和。

子数组是数组中的一个连续部分。

**进阶：**如果你已经实现复杂度为 O(n) 的解法，尝试使用更为精妙的 分治法 求解。

提示：

1 <= nums.length <= 105

104 <= nums[i] <= 104

示例：

1
2
3
4
5
6
7
8
9
输入：nums = [-2,1,-3,4,-1,2,1,-5,4]
输出：6
解释：连续子数组 [4,-1,2,1] 的和最大，为 6 。

输入：nums = [1]
输出：1

输入：nums = [5,4,-1,7,8]
输出：23

代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
/**
 * 寻找连续子数组中的最大和
 * 本方法实现了一种寻找最大和的高效算法，其核心思想是通过不断累加当前元素并比较累加和，
 * 来确定最大子数组的和这种方法被称为Kadane算法
 * 
 * @param nums 这是一个整数数组，其中包含我们要分析的数字
 * @return 返回连续子数组的最大和
 */
public int maxSubArray(int[] nums) {
    // 初始化最大和为最小整数值，确保任何子数组的和都会比初始值大
    int ans = Integer.MIN_VALUE;
    // sum用于记录当前子数组的累加和
    int sum = 0;
    // 遍历数组中的每个元素
    for (int num : nums) {
        // 如果当前累加和小于等于零，重新开始累加，因为负数对后续元素的累加没有贡献
        if (sum <= 0) {
            sum = num;
        } else {
            // 如果当前累加和大于零，继续累加当前元素
            sum += num;
        }
        // 比较并更新最大子数组的和
        ans = Math.max(ans, sum);
    }
    // 返回最大子数组的和
    return ans;
}

2. 合并区间

以数组 intervals 表示若干个区间的集合，其中单个区间为 intervals[i] = [starti, endi] 。请你合并所有重叠的区间，并返回 一个不重叠的区间数组，该数组需恰好覆盖输入中的所有区间 。

提示：

1 <= intervals.length <= 104

intervals[i].length == 2

0 <= starti <= endi <= 104

示例：

1
2
3
4
5
6
7
输入：intervals = [[1,3],[2,6],[8,10],[15,18]]
输出：[[1,6],[8,10],[15,18]]
解释：区间 [1,3] 和 [2,6] 重叠, 将它们合并为 [1,6].

输入：intervals = [[1,4],[4,5]]
输出：[[1,5]]
解释：区间 [1,4] 和 [4,5] 可被视为重叠区间。

代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
public int[][] merge(int[][] intervals) {
    List<int[]> list = new ArrayList<>();
    PriorityQueue<int[]> pq = new PriorityQueue<>((a, b) -> a[0] != b[0] ? a[0] - b[0] : a[1] - b[1]);
    pq.addAll(Arrays.asList(intervals));
    while (!pq.isEmpty()) {
        int[] cur = pq.poll();
        int[] res = new int[2];
        res[0] = cur[0];
        res[1] = cur[1];
        list.add(res);
        while (!pq.isEmpty()) {
            int[] peek = pq.peek();
            if (cur[1] >= peek[0] || res[1] >= peek[0]) {
                res[0] = Math.min(peek[0], res[0]);
                res[1] = Math.max(pq.poll()[1], res[1]);
            } else {
                break;
            }
        }
    }

    return list.toArray(new int[list.size()][]);
}

 /**
 * 如果输入区间为空，返回空数组。
 * 按照区间的起始位置对区间进行排序。
 * 遍历排序后的区间列表，检查当前区间是否与前一个区间重叠。如果不重叠，则将当前区间加入结果列表；如果重叠，则更新前一个区间的结束位置为两者结束位置的最大值。
 * 最后将结果列表转换为二维数组并返回。
 * @param intervals 区间列表
 * @return      
 */
public int[][] merge(int[][] intervals) {
    if (intervals.length == 0) {
        return new int[0][2];
    }
    Arrays.sort(intervals, new Comparator<int[]>() {
        public int compare(int[] interval1, int[] interval2) {
            return interval1[0] - interval2[0];
        }
    });
    List<int[]> merged = new ArrayList<int[]>();
    for (int i = 0; i < intervals.length; ++i) {
        int L = intervals[i][0], R = intervals[i][1];
        if (merged.size() == 0 || merged.get(merged.size() - 1)[1] < L) {
            merged.add(new int[]{L, R});
        } else {
            merged.get(merged.size() - 1)[1] = Math.max(merged.get(merged.size() - 1)[1], R);
        }
    }
    return merged.toArray(new int[merged.size()][]);
}

3. 轮转数组

给定一个整数数组 nums，将数组中的元素向右轮转 k **个位置，其中 k **是非负数。

  • 尽可能想出更多的解决方案，至少有 三种 不同的方法可以解决这个问题。
  • 你可以使用空间复杂度为 O(1) 的 原地 算法解决这个问题吗？

提示：

1 <= nums.length <= 105

231 <= nums[i] <= 231 - 1

0 <= k <= 105

示例：

1
2
3
4
5
6
7
8
9
10
11
12
输入: nums = [1,2,3,4,5,6,7], k = 3
输出: [5,6,7,1,2,3,4]
解释:
向右轮转 1 步: [7,1,2,3,4,5,6]
向右轮转 2 步: [6,7,1,2,3,4,5]
向右轮转 3 步: [5,6,7,1,2,3,4]

输入：nums = [-1,-100,3,99], k = 2
输出：[3,99,-1,-100]
解释: 
向右轮转 1 步: [99,-1,-100,3]
向右轮转 2 步: [3,99,-1,-100]

代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
// 数组翻转
public void rotate(int[] nums, int k) {
    k %=nums.length;
    reverse(nums, 0, nums.length - 1);
    reverse(nums, 0, k - 1);
    reverse(nums, k, nums.length - 1);
}

public void reverse(int[] nums, int start, int end) {
    while (start < end) {
        int temp = nums[start];
        nums[start] = nums[end];
        nums[end] = temp;
        start += 1;
        end -= 1;
    }
}

4. 除自身以外数组的乘积

【数组】、【前缀和】

给你一个整数数组 nums，返回 数组 answer ，其中 answer[i] 等于 nums 中除 nums[i] 之外其余各元素的乘积 。

题目数据 保证 数组 nums之中任意元素的全部前缀元素和后缀的乘积都在  32 位 整数范围内。

请 **不要使用除法，**且在 O(n) 时间复杂度内完成此题。

**进阶：**你可以在 O(1) 的额外空间复杂度内完成这个题目吗？（ 出于对空间复杂度分析的目的，输出数组 不被视为 额外空间。）

提示：

2 <= nums.length <= 105

30 <= nums[i] <= 30

输入 保证 数组 answer[i] 在 32 位 整数范围内

示例：

1
2
3
4
5
输入: nums = [1,2,3,4]
输出: [24,12,8,6]

输入: nums = [-1,1,0,-3,3]
输出: [0,0,9,0,0]

代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
/**
 * 计算除自身以外所有元素的乘积数组
 * 该方法通过两次遍历数组，第一次从左到右，第二次从右到左，来计算每个元素左侧和右侧所有元素的乘积
 * 这样做避免了使用除法，可以在不使用额外空间（除结果数组外）的情况下解决问题
 *
 * @param nums 输入的整数数组
 * @return 返回一个数组，其中每个元素为原数组中除自身以外所有元素的乘积
 */
public int[] productExceptSelf(int[] nums) {
    // 初始化结果数组，初始值都为1，因为后续操作是乘法，初始值设为1不会影响最终结果
    int[] res = new int[nums.length];
    Arrays.fill(res, 1);
    
    // 初始化左侧乘积为1，表示第一个元素左边没有元素
    int left = 1;
    // 初始化右侧乘积为1，表示最后一个元素右边没有元素
    int right = 1;
    
    // 从左到右遍历数组，计算每个元素左侧所有元素的乘积
    for (int i = 0; i < nums.length; i++) {
        // 更新当前元素的值为原值乘以左侧乘积
        res[i] = res[i] * left;
        // 更新左侧乘积为当前元素的值乘以左侧乘积
        left = left * nums[i];
    }
    
    // 打印左侧乘积结果，用于调试
    //System.out.printf(Arrays.toString(res));
    
    // 从右到左遍历数组，计算每个元素右侧所有元素的乘积
    for (int i = nums.length - 1; i >= 0; i--) {
        // 更新当前元素的值为原值乘以右侧乘积
        res[i] = res[i] * right;
        // 更新右侧乘积为当前元素的值乘以右侧乘积
        right = right * nums[i];
    }
    
    // 返回结果数组，其中每个元素都是除自身以外所有元素的乘积
    return res;
}

5. 缺失的第一个正数

【数组】，【哈希】

给你一个未排序的整数数组 nums ，请你找出其中没有出现的最小的正整数。

请你实现时间复杂度为O(n)并且只使用常数级别额外空间的解决方案。

提示：

1 <= nums.length <= 105

231 <= nums[i] <= 231 - 1

示例：

1
2
3
4
5
6
7
8
9
10
11
输入：nums = [1,2,0]
输出：3
解释：范围 [1,2] 中的数字都在数组中。

输入：nums = [3,4,-1,1]
输出：2
解释：1 在数组中，但 2 没有。

输入：nums = [7,8,9,11,12]
输出：1
解释：最小的正数 1 没有出现。

代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
/**
 * 寻找第一个缺失的正整数
 * 该方法旨在找出数组中第一个缺失的正整数，数字从1开始计数
 * 通过修改原数组实现，不使用额外空间
 *
 * @param nums 输入的整数数组
 * @return 返回第一个缺失的正整数
 */
public int firstMissingPositive(int[] nums) {
    // 遍历数组，将非正整数替换为一个超出数组长度的值
    // 这样做是为了忽略非正整数和超出数组长度的值，因为它们不会影响到第一个缺失的正整数
    for (int i = 0; i < nums.length; i++) {
        if (nums[i] <= 0) {
            nums[i] = nums.length + 1;
        }
    }
    
    // 再次遍历数组，将数组中值为正且不超过数组长度的数对应的位置标记为负数
    // 通过将索引对应的值设为负数，来标记这个索引+1（因为数组从0索引开始）的数存在
    for (int i = 0; i < nums.length; i++) {
        int num = Math.abs(nums[i]);
        if (num <= nums.length) {
            nums[num - 1] = -Math.abs(nums[num - 1]);
        }
    }
    
    // 最后遍历数组，找到第一个正数，这表示这个位置的索引+1的数缺失
    // 如果整个数组都是负数，则说明1到nums.length的数都在数组中，返回nums.length + 1
    for (int i = 0; i < nums.length; i++) {
        if (nums[i] > 0) {
            return i + 1;
        }
    }
    
    // 如果数组中所有的数都被标记为负数，说明缺失的第一个正整数是nums.length + 1
    return nums.length + 1;
}

6. 数组中的第K个最大元素

【数组】，【分治】、【快速选择】、【排序】、【堆】

给定整数数组 nums 和整数 k，请返回数组中第 **k** 个最大的元素。

请注意，你需要找的是数组排序后的第 k 个最大的元素，而不是第 k 个不同的元素。

你必须设计并实现时间复杂度为 O(n) 的算法解决此问题。

提示：

1 <= k <= nums.length <= 105

-104 <= nums[i] <= 104

示例：

1
2
3
4
5
输入: [3,2,1,5,6,4], k = 2
输出: 5

输入: [3,2,3,1,2,4,5,5,6], k = 4
输出: 4

代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33

class Solution {
    
    // 实现快速选择
    int quickselect(int[] nums, int l, int r, int k) {
        if (l == r) {
            return nums[k];
        }
        int x = nums[l], i = l - 1, j = r + 1;
        while (i < j) {
            do {
                i++;
            } while (nums[i] < x);
            do {
                j--;
            } while (nums[j] > x);
            if (i < j) {
                int tmp = nums[i];
                nums[i] = nums[j];
                nums[j] = tmp;
            }
        }
        if (k <= j) {
            return quickselect(nums, l, j, k);
        }
        return quickselect(nums, j + 1, r, k);
    }

    public int findKthLargest(int[] _nums, int k) {
        int n = _nums.length;
        return quickselect(_nums, 0, n - 1, n - k);
    }
}

矩阵

1. 矩阵置零

【数组】，【哈希表】，【矩阵】

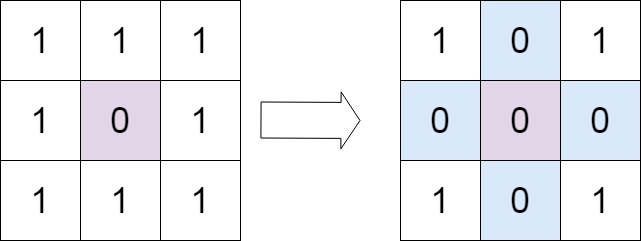
给定一个 *m* x *n* 的矩阵，如果一个元素为 0 ，则将其所在行和列的所有元素都设为 0 。请使用 原地 算法**。**

进阶：

  • 一个直观的解决方案是使用 O(*mn*) 的额外空间，但这并不是一个好的解决方案。
  • 一个简单的改进方案是使用 O(*m* + *n*) 的额外空间，但这仍然不是最好的解决方案。
  • 你能想出一个仅使用常量空间的解决方案吗？

提示：

m == matrix.length

n == matrix[0].length

1 <= m, n <= 200

231 <= matrix[i][j] <= 231 - 1

示例：

image.png

1
2
输入：matrix = [[1,1,1],[1,0,1],[1,1,1]]
输出：[[1,0,1],[0,0,0],[1,0,1]]

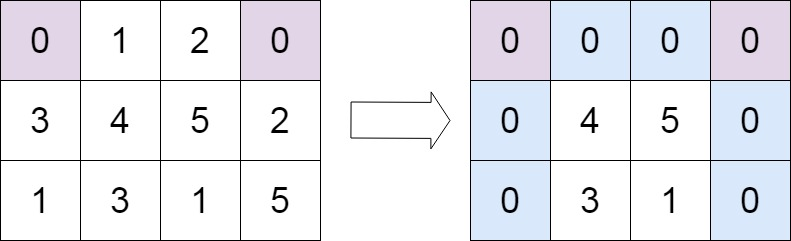
image.png

1
2
输入：matrix = [[0,1,2,0],[3,4,5,2],[1,3,1,5]]
输出：[[0,0,0,0],[0,4,5,0],[0,3,1,0]]

代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
public void setZeroes(int[][] matrix) {
    // 标记第一行和第一列是否需要置为0
    boolean isFirstRowZero = false;
    boolean isFirstColZero = false;
    
    // 检查第一列是否有0
    for (int i = 0; i < matrix.length; i++) {
        if (matrix[i][0] == 0) {
            isFirstColZero = true;
            break;
        }
    }
    
    // 检查第一行是否有0
    for (int j = 0; j < matrix[0].length; j++) {
        if (matrix[0][j] == 0) {
            isFirstRowZero = true;
            break;
        }
    }
    
    // 使用第一行和第一列记录每行和每列是否需要置为0
    for (int i = 1; i < matrix.length; i++) {
        for (int j = 1; j < matrix[i].length; j++) {
            if (matrix[i][j] == 0) {
                matrix[i][0] = 0;
                matrix[0][j] = 0;
            }
        }
    }
    
    // 根据第一行和第一列的信息，将相应行和列置为0
    for (int i = 1; i < matrix.length; i++) {
        if (matrix[i][0] == 0) {
            Arrays.fill(matrix[i], 0);
        }
    }
    
    for (int j = 1; j < matrix[0].length; j++) {
        if (matrix[0][j] == 0) {
            for (int i = 0; i < matrix.length; i++) {
                matrix[i][j] = 0;
            }
        }
    }
    
    // 最后处理第一行和第一列
    if (isFirstRowZero) {
        Arrays.fill(matrix[0], 0);
    }
    
    if (isFirstColZero) {
        for (int i = 0; i < matrix.length; i++) {
            matrix[i][0] = 0;
        }
    }
}

2. 螺旋矩阵

【数组】，【矩阵】，【模拟】

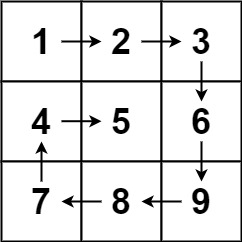
给你一个 m 行 n 列的矩阵 matrix ，请按照 顺时针螺旋顺序 ，返回矩阵中的所有元素。

提示：

m == matrix.length

n == matrix[i].length

1 <= m, n <= 10

100 <= matrix[i][j] <= 100

示例：

image.png

1
2
输入：matrix = [[1,2,3],[4,5,6],[7,8,9]]
输出：[1,2,3,6,9,8,7,4,5]

image.png

1
2
输入：matrix = [[1,2,3,4],[5,6,7,8],[9,10,11,12]]
输出：[1,2,3,4,8,12,11,10,9,5,6,7]

代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
public List<Integer> spiralOrder(int[][] matrix) {
    List<Integer> res = new ArrayList<>();
    
    // 检查输入矩阵是否为空或非法
    if (matrix == null || matrix.length == 0 || matrix[0].length == 0) {
        return res;
    }
    
    int rows = matrix.length;
    int cols = matrix[0].length;
    int top = 0, bottom = rows - 1, left = 0, right = cols - 1;
    
    while (top <= bottom && left <= right) {
        // 从左到右遍历上边行
        for (int i = left; i <= right; i++) {
            res.add(matrix[top][i]);
        }
        top++;
        
        // 从上到下遍历右边列
        for (int i = top; i <= bottom; i++) {
            res.add(matrix[i][right]);
        }
        right--;
        
        // 从右到左遍历下边行
        if (top <= bottom) {
            for (int i = right; i >= left; i--) {
                res.add(matrix[bottom][i]);
            }
            bottom--;
        }
        
        // 从下到上遍历左边列
        if (left <= right) {
            for (int i = bottom; i >= top; i--) {
                res.add(matrix[i][left]);
            }
            left++;
        }
    }
    
    return res;
}

3. 旋转图像

【数组】，【数学】，【矩阵】

给定一个 n × n 的二维矩阵 matrix 表示一个图像。请你将图像顺时针旋转 90 度。

你必须在 原地 旋转图像，这意味着你需要直接修改输入的二维矩阵。请不要 使用另一个矩阵来旋转图像。

提示：

n == matrix.length == matrix[i].length

1 <= n <= 20

1000 <= matrix[i][j] <= 1000

示例：

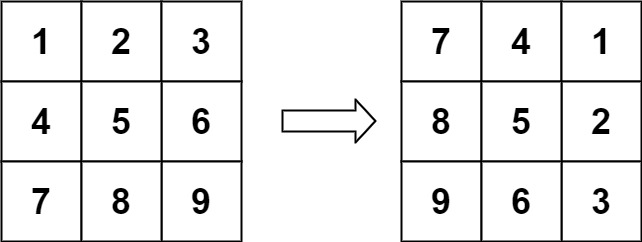
image.png

1
2
输入：matrix = [[1,2,3],[4,5,6],[7,8,9]]
输出：[[7,4,1],[8,5,2],[9,6,3]]

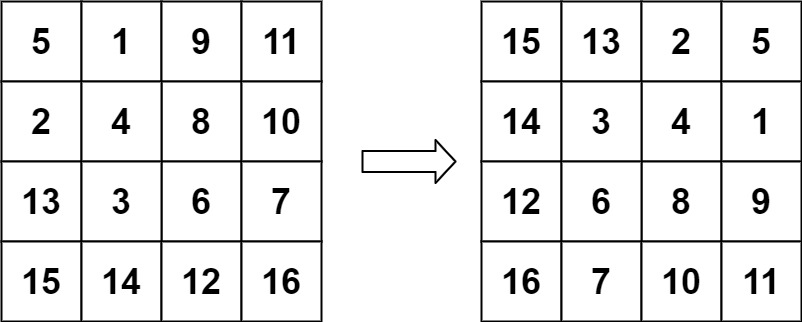
image.png

1
2
输入：matrix = [[5,1,9,11],[2,4,8,10],[13,3,6,7],[15,14,12,16]]
输出：[[15,13,2,5],[14,3,4,1],[12,6,8,9],[16,7,10,11]]

代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
/**
 * 旋转图像
 *
 * @param matrix 输入的二维数组
 */
public void rotate(int[][] matrix) {
    // 获取矩阵的长度
    int n = matrix.length;
    
    // 外层循环遍历矩阵的一半，因为一次旋转操作会涉及四个角的位置变换
    for (int i = 0; i < n / 2; i++) {
        // 内层循环遍历稍多于一半的列，确保每个元素都被旋转到正确的位置
        for (int j = 0; j < (n + 1) / 2; j++) {
            // 保存当前元素的值，用于交换
            int tmp = matrix[i][j];
            // 将左侧的值旋转到当前位置
            matrix[i][j] = matrix[n - 1 - j][i];
            // 将底部的值旋转到左侧的位置
            matrix[n - 1 - j][i] = matrix[n - 1 - i][n - 1 - j];
            // 将右侧的值旋转到底部的位置
            matrix[n - 1 - i][n - 1 - j] = matrix[j][n - 1 - i];
            // 将之前保存的顶部值旋转到右侧的位置，完成一次旋转操作
            matrix[j][n - 1 - i] = tmp;
        }
    }
}

4. 搜索二维矩阵 II

【数组】、【二分查找】、【分治】、【矩阵】

编写一个高效的算法来搜索 *m* x *n* 矩阵 matrix 中的一个目标值 target 。该矩阵具有以下特性：

  • 每行的元素从左到右升序排列。
  • 每列的元素从上到下升序排列。

提示：

m == matrix.length

n == matrix[i].length

1 <= n, m <= 300

109 <= matrix[i][j] <= 109

每行的所有元素从左到右升序排列

每列的所有元素从上到下升序排列

109 <= target <= 109

示例：

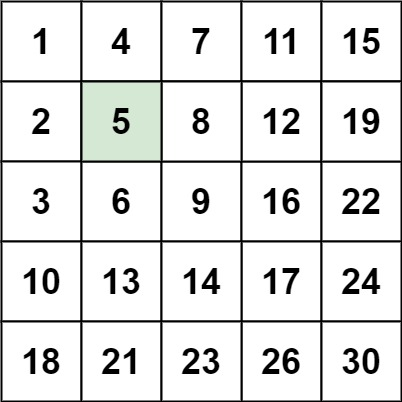
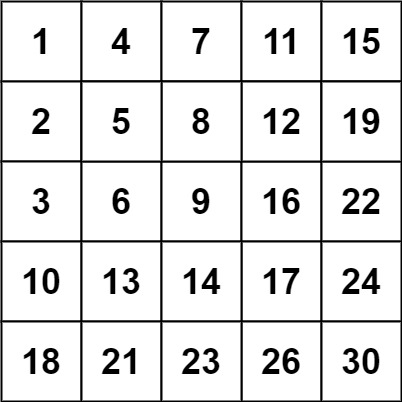
image.png

1
2
输入：matrix = [[1,4,7,11,15],[2,5,8,12,19],[3,6,9,16,22],[10,13,14,17,24],[18,21,23,26,30]], target = 5
输出：true

image.png

1
2
输入：matrix = [[1,4,7,11,15],[2,5,8,12,19],[3,6,9,16,22],[10,13,14,17,24],[18,21,23,26,30]], target = 20
输出：false

代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
/**
 * 方法一：
 * 在一个二维矩阵中搜索一个特定的目标值
 * 矩阵的每一行都被认为是升序排列的
 * 
 * @param matrix 一个二维矩阵，其中每个子数组代表矩阵的一行
 * @param target 要搜索的目标值
 * @return 如果目标值在矩阵中找到，则返回true；否则返回false
 */
public boolean searchMatrix(int[][] matrix, int target) {
    // 初始化搜索的上下边界
    int top = 0, bottom = matrix.length - 1;
    // 当上边界不超过下边界时，执行搜索
    while (top <= bottom) {
        // 初始化搜索的左右边界
        int left = 0, right = matrix[0].length - 1;
        // 当左边界不超过右边界且右边界最大值大于等于目标值时，执行搜索
        while (left <= right && matrix[top][right] >= target) {
            // 计算中间位置
            int mid = (left + right) / 2;
            // 如果中间位置的值等于目标值，返回true
            if (matrix[top][mid] == target) {
                return true;
            } else if (matrix[top][mid] > target) {
                // 如果中间位置的值大于目标值，调整右边界
                right = mid - 1;
            } else {
                // 如果中间位置的值小于目标值，调整左边界
                left = mid + 1;
            }
        }
        // 移动上边界，准备搜索下一行
        top++;
        // 如果最左侧的值大于目标值，调整下边界
        if (matrix[bottom][0] > target) {
            bottom--;
        }
    }
    // 如果没有找到目标值，返回false
    return false;
}

/**
 * 方法二：
 * 在一个二维矩阵中搜索一个特定的目标值
 * 该矩阵的特点是每行从左到右递增，每列从上到下递增
 * 此方法利用矩阵的排序特性来高效搜索目标值
 * 
 * @param matrix 一个二维整数数组，表示待搜索的矩阵
 * @param target 一个整数，表示要搜索的目标值
 * @return 如果矩阵中存在该目标值，则返回true；否则返回false
 */
public boolean searchMatrix(int[][] matrix, int target) {
    // 初始化搜索的起始位置在矩阵的左下角
    int left = 0, bottom = matrix.length - 1;
    
    // 当搜索位置没有越界时，继续搜索
    while (left <= matrix[0].length - 1 && bottom >= 0) {
        // 如果找到目标值，返回true
        if (matrix[bottom][left] == target) {
            return true;
        }
        // 如果当前位置的值大于目标值，说明目标值可能在上方，向上移动一行
        if (matrix[bottom][left] > target) {
            bottom--;
        } else {
            // 如果当前位置的值小于目标值，说明目标值可能在右方，向右移动一列
            left++;
        }
    }
    // 如果搜索完整个矩阵都没有找到目标值，返回false
    return false;
}

链表

1. 相交链表

【】，【】

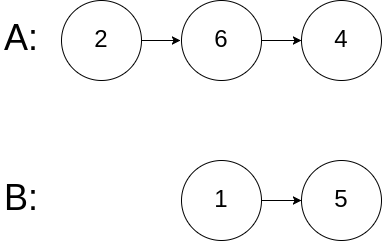
给你两个单链表的头节点 headA 和 headB ，请你找出并返回两个单链表相交的起始节点。如果两个链表不存在相交节点，返回 null 。

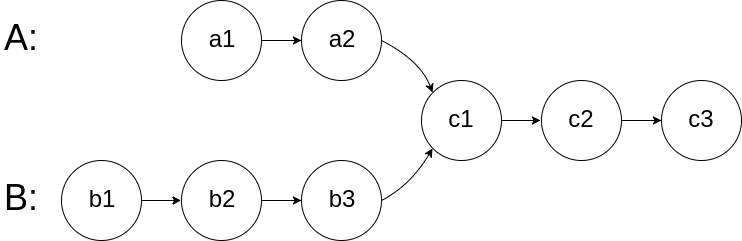
图示两个链表在节点 c1 开始相交**：**

image.png

题目数据 保证 整个链式结构中不存在环。

注意，函数返回结果后，链表必须 保持其原始结构 。

自定义评测：

评测系统 的输入如下（你设计的程序 不适用 此输入）：

  • intersectVal - 相交的起始节点的值。如果不存在相交节点，这一值为 0
  • listA - 第一个链表
  • listB - 第二个链表
  • skipA - 在 listA 中（从头节点开始）跳到交叉节点的节点数
  • skipB - 在 listB 中（从头节点开始）跳到交叉节点的节点数

评测系统将根据这些输入创建链式数据结构，并将两个头节点 headA 和 headB 传递给你的程序。如果程序能够正确返回相交节点，那么你的解决方案将被 视作正确答案 。

**进阶：**你能否设计一个时间复杂度 O(m + n) 、仅用 O(1) 内存的解决方案？

提示：

listA 中节点数目为 m

listB 中节点数目为 n

1 <= m, n <= 3 * 104

1 <= Node.val <= 105

0 <= skipA <= m

0 <= skipB <= n

如果 listA 和 listB 没有交点，intersectVal 为 0

如果 listA 和 listB 有交点，intersectVal == listA[skipA] == listB[skipB]

示例：

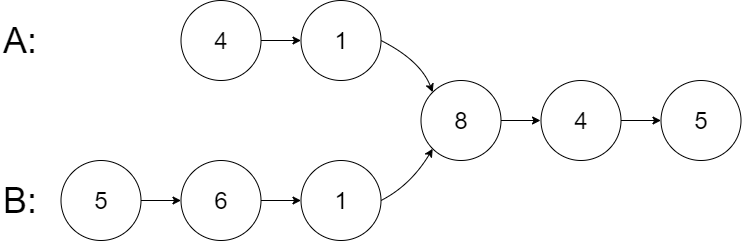
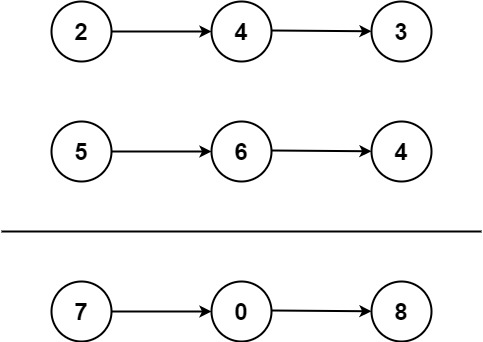
image.png

1
2
3
4
5
6
输入：intersectVal = 8, listA = [4,1,8,4,5], listB = [5,6,1,8,4,5], skipA = 2, skipB = 3
输出：Intersected at '8'
解释：相交节点的值为 8 （注意，如果两个链表相交则不能为 0）。
从各自的表头开始算起，链表 A 为 [4,1,8,4,5]，链表 B 为 [5,6,1,8,4,5]。
在 A 中，相交节点前有 2 个节点；在 B 中，相交节点前有 3 个节点。
— 请注意相交节点的值不为 1，因为在链表 A 和链表 B 之中值为 1 的节点 (A 中第二个节点和 B 中第三个节点) 是不同的节点。换句话说，它们在内存中指向两个不同的位置，而链表 A 和链表 B 中值为 8 的节点 (A 中第三个节点，B 中第四个节点) 在内存中指向相同的位置。

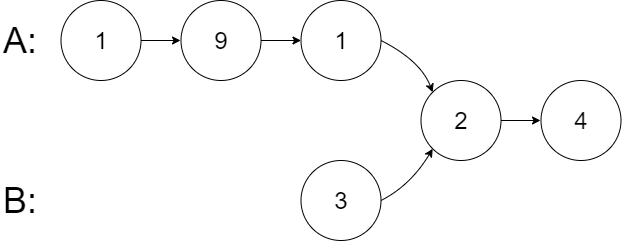
image.png

1
2
3
4
5
输入：intersectVal = 2, listA = [1,9,1,2,4], listB = [3,2,4], skipA = 3, skipB = 1
输出：Intersected at '2'
解释：相交节点的值为 2 （注意，如果两个链表相交则不能为 0）。
从各自的表头开始算起，链表 A 为 [1,9,1,2,4]，链表 B 为 [3,2,4]。
在 A 中，相交节点前有 3 个节点；在 B 中，相交节点前有 1 个节点。

image.png

1
2
3
4
5
输入：intersectVal = 0, listA = [2,6,4], listB = [1,5], skipA = 3, skipB = 2
输出：No intersection
解释：从各自的表头开始算起，链表 A 为 [2,6,4]，链表 B 为 [1,5]。
由于这两个链表不相交，所以 intersectVal 必须为 0，而 skipA 和 skipB 可以是任意值。
这两个链表不相交，因此返回 null 。

代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
/**
 * 获取两个链表的交点节点
 * 如果两个链表有交点，则从交点开始，两个链表的节点是一样的
 * 解决这个问题的关键在于，通过某种方式让两个链表的长度相等，然后同步遍历两个链表，找到第一个相同的节点
 * 本方法的巧妙之处在于，不需要真的去计算两个链表的长度差，而是通过交换遍历的方式，自然地抵消了长度差
 * 
 * @param headA 第一个链表的头节点
 * @param headB 第二个链表的头节点
 * @return 返回两个链表的交点节点，如果没有交点，则返回null
 */
public ListNode getIntersectionNode(ListNode headA, ListNode headB) {
    // 如果任一链表为空，则不可能有交点，直接返回null
    if (headA == null || headB == null) {
        return null;
    }
    
    // 初始化两个指针，分别指向两个链表的头节点
    ListNode a = headA, b = headB;
    
    // 遍历两个链表，当任一指针不为空时继续循环
    while (a != null || b != null) {
        // 如果两个指针指向相同的节点，说明找到了交点，返回该节点
        if (a == b) {
            return a;
        }
        
        // 移动指针，如果指针a到达链表A的末尾，则将其指向链表B的头节点；否则继续向下移动
        a = a == null ? headB : a.next;
        
        // 移动指针，如果指针b到达链表B的末尾，则将其指向链表A的头节点；否则继续向下移动
        b = b == null ? headA : b.next;
    }
    
    // 如果两个链表没有交点，则返回null
    return null;
}

/**
 * 获取两个链表的交点节点
 * 
 * @param headA 第一个链表的头节点
 * @param headB 第二个链表的头节点
 * @return 返回交点节点，如果没有交点则返回null
 */
public ListNode getIntersectionNode(ListNode headA, ListNode headB) {
    // 初始化两个指针aList和bList分别指向两个链表的头节点
    ListNode aList = headA;
    ListNode bList = headB;

    // 第一次遍历两个链表，分别移动指针直到其中一个链表结束
    while (aList != null && bList != null) {
        aList = aList.next;
        bList = bList.next;
    }

    // 如果aList链表更长，将headA移动到与headB相同长度的位置
    while (aList != null) {
        headA = headA.next;
        aList = aList.next;
    }

    // 如果bList链表更长，将headB移动到与headA相同长度的位置
    while (bList != null) {
        headB = headB.next;
        bList = bList.next;
    }

    // 同时遍历两个链表，直到找到相同的节点（即交点）
    while (headA != headB) {
        headA = headA.next;
        headB = headB.next;
    }

    // 返回交点节点，如果没有交点则返回null
    return headA;
}

2. 反转链表

【递归】、【链表】

给你单链表的头节点 head ，请你反转链表，并返回反转后的链表。

**进阶：**链表可以选用迭代或递归方式完成反转。你能否用两种方法解决这道题？

提示：

链表中节点的数目范围是 [0, 5000]

5000 <= Node.val <= 5000

示例：

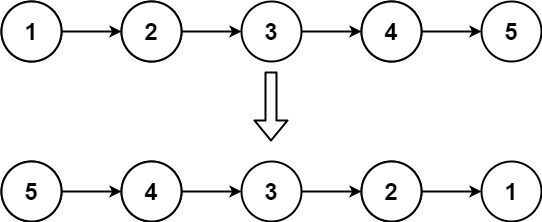
image.png

1
2
输入：head = [1,2,3,4,5]
输出：[5,4,3,2,1]

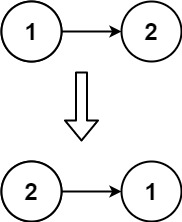
image.png

1
2
输入：head = [1,2]
输出：[2,1]
1
2
输入：head = []
输出：[]

代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
/**
 * 反转一个单链表, 迭代方式
 * 此方法通过迭代方式反转链表，不需要额外的存储空间，直接在原链表上进行操作
 * 
 * @param head 链表的头节点如果链表为空或只有一个节点，则直接返回该节点
 * @return 反转后的链表的头节点
 */
public ListNode reverseList(ListNode head) {
    // 检查链表是否为空或只有一个节点，如果是，直接返回
    if (head == null || head.next == null) {
        return head;
    }
    
    // 初始化前一个节点pre，这里创建了一个新节点，其值与头节点相同
    // 这个操作实际上是多余的，可以在进入循环后直接操作，这里可能是为了简化逻辑
    ListNode pre = new ListNode(head.val);
    
    // 遍历链表，直到最后一个节点
    while (head.next != null) {
        // 创建当前节点current，复制下一个节点的值
        // 这种创建方式保证了不会改变原链表的结构
        ListNode current = new ListNode(head.next.val);
        // 移动head指针到下一个节点，为下一次迭代做准备
        head = head.next;
        // 将当前节点指向前面的节点，实现反转
        current.next = pre;
        // 更新pre指针，指向当前节点，为下一次迭代做准备
        pre = current;
    }
    
    // 返回反转后的链表的头节点
    return pre;
}

3. 回文链表

【栈】、【递归】、【链表】、【双指针】

给你一个单链表的头节点 head ，请你判断该链表是否为回文链表。如果是，返回 true ；否则，返回 false 。

提示：

链表中节点数目在范围[1, 105] 内

0 <= Node.val <= 9

示例：

image.png

1
2
输入：head = [1,2,2,1]
输出：true

image.png

1
2
输入：head = [1,2]
输出：false

代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
public ListNode reverseList(ListNode head) {
    if (head == null || head.next == null) {
        return head;
    }
    ListNode cur = head;
    ListNode pre = null;
    while (cur != null) {
        ListNode next = cur.next;
        cur.next = pre;
        pre = cur;
        cur = next;
    }
    return pre;
}

/**
 * 判断一个链表是否为回文链表
 * 
 * @param head 链表的头节点
 * @return 如果链表是回文的，返回true；否则返回false
 */
public boolean isPalindrome(ListNode head) {
    // 如果链表为空或只有一个节点，它是回文链表
    if (head == null || head.next == null) {
        return true;
    }
    
    // 使用快慢指针找到链表的中点
    ListNode fast = head;
    ListNode slow = head;
    // 当快指针到达链表末尾时，慢指针正好在链表中点
    while (fast.next != null && fast.next.next != null) {
        fast = fast.next.next;
        slow = slow.next;
    }
    
    // 反转链表的后半部分
    ListNode listNode = reverseList(slow.next);
    // 比较前半部分和反转后的后半部分是否相同
    while (listNode != null) {
        if (listNode.val != head.val) {
            return false;
        }
        listNode = listNode.next;
        head = head.next;
    }
    
    // 如果所有节点匹配成功，则链表是回文的
    return true;
}

4. 两数相加

【递归】、【链表】、【数学】

给你单链表的头节点 head ，请你反转链表，并返回反转后的链表

提示：

每个链表中的节点数在范围 [1, 100] 内

0 <= Node.val <= 9

题目数据保证列表表示的数字不含前导零

示例：

image.png

1
2
3
输入：l1 = [2,4,3], l2 = [5,6,4]
输出：[7,0,8]
解释：342 + 465 = 807
1
2
输入：l1 = [0], l2 = [0]
输出：[0]
1
2
输入：l1 = [9,9,9,9,9,9,9], l2 = [9,9,9,9]
输出：[8,9,9,9,0,0,0,1]

代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
public ListNode addTwoNumbers(ListNode l1, ListNode l2) {
       ListNode dummyHead = new ListNode();
       ListNode current = dummyHead;
       int carry = 0;

       while (l1 != null || l2 != null || carry != 0) {
           int sum = carry;
           if (l1 != null) {
               sum += l1.val;
               l1 = l1.next;
           }
           if (l2 != null) {
               sum += l2.val;
               l2 = l2.next;
           }
           carry = sum / 10;
           current.next = new ListNode(sum % 10);
           current = current.next;
       }

       return dummyHead.next;
   }

5. 环形链表

【哈希表】、【链表】、【双指针】

给你一个链表的头节点 head ，判断链表中是否有环。

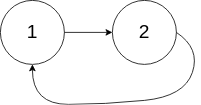
如果链表中有某个节点，可以通过连续跟踪 next 指针再次到达，则链表中存在环。 为了表示给定链表中的环，评测系统内部使用整数 pos 来表示链表尾连接到链表中的位置（索引从 0 开始）。注意：pos 不作为参数进行传递 。仅仅是为了标识链表的实际情况。

如果链表中存在环 ，则返回 true 。 否则，返回 false 。

**进阶：**你能用 O(1)（即，常量）内存解决此问题吗？

提示：

链表中节点的数目范围是 [0, 104]

105 <= Node.val <= 105

pos 为 1 或者链表中的一个 有效索引 。

示例：

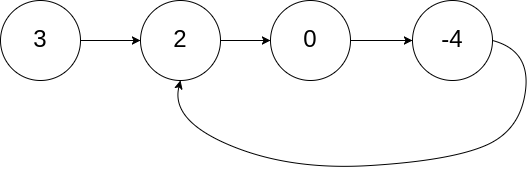
image.png

1
2
3
输入：head = [3,2,0,-4], pos = 1
输出：true
解释：链表中有一个环，其尾部连接到第二个节点。

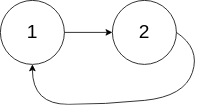
image.png

1
2
3
输入：head = [1,2], pos = 0
输出：true
解释：链表中有一个环，其尾部连接到第一个节点。

image.png

1
2
3
输入：head = [1], pos = -1
输出：false
解释：链表中没有环。

代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
public boolean hasCycle(ListNode head) {
     if (head == null || head.next == null) {
         return false;
     }
     ListNode fast = head.next;
     ListNode slow = head;
     while(fast != slow) {
         if (fast == null || fast.next == null) {
             return false;
         }
         fast = fast.next.next;
         slow = slow.next;
     }
     return true;
 }

6. 环形链表Ⅱ

【哈希表】、【链表】、【双指针】

给定一个链表的头节点  head ，返回链表开始入环的第一个节点。 如果链表无环，则返回 null。

如果链表中有某个节点，可以通过连续跟踪 next 指针再次到达，则链表中存在环。 为了表示给定链表中的环，评测系统内部使用整数 pos 来表示链表尾连接到链表中的位置（索引从 0 开始）。如果 pos 是 -1，则在该链表中没有环。注意：pos 不作为参数进行传递，仅仅是为了标识链表的实际情况。

不允许修改 链表。

**进阶：**你是否可以使用 O(1) 空间解决此题？

提示：

链表中节点的数目范围在范围 [0, 104] 内

105 <= Node.val <= 105

pos 的值为 1 或者链表中的一个有效索引

示例：

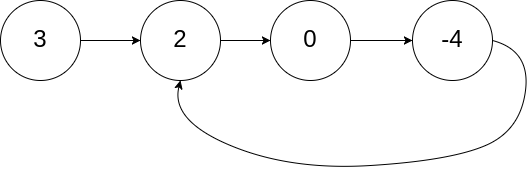
image.png

1
2
3
输入：head = [3,2,0,-4], pos = 1
输出：返回索引为 1 的链表节点
解释：链表中有一个环，其尾部连接到第二个节点。

image.png

1
2
3
输入：head = [1,2], pos = 0
输出：返回索引为 0 的链表节点
解释：链表中有一个环，其尾部连接到第一个节点。

image.png

1
2
3
输入：head = [1], pos = -1
输出：返回 null
解释：链表中没有环。

代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
public ListNode detectCycle(ListNode head) {
    if (head == null || head.next == null) {
        return null;
    }
    ListNode fast = head;
    ListNode slow = head;
    while(fast != null && fast.next != null&& slow.next != null) {
        fast = fast.next.next;
        slow = slow.next;
        if (fast == slow) {
            ListNode pre = head;
            while(pre != slow) {
                pre = pre.next;
                slow = slow.next;
            }
            return pre;
        }
    }
    return null;
}

7. K 个一组翻转链表

【递归】、【链表】

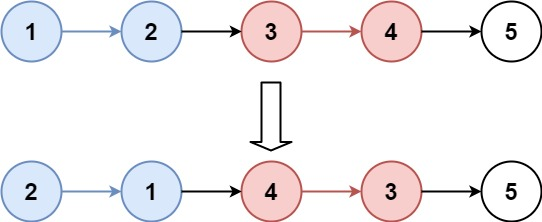
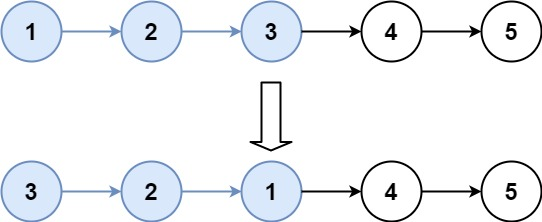
给你链表的头节点 head ，每 k **个节点一组进行翻转，请你返回修改后的链表。

k 是一个正整数，它的值小于或等于链表的长度。如果节点总数不是 k **的整数倍，那么请将最后剩余的节点保持原有顺序。

你不能只是单纯的改变节点内部的值，而是需要实际进行节点交换。

**进阶：**你可以设计一个只用 O(1) 额外内存空间的算法解决此问题吗？

提示：

链表中的节点数目为 n

1 <= k <= n <= 5000

0 <= Node.val <= 1000

示例：

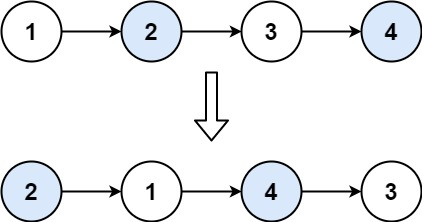
image.png

1
2
输入：head = [1,2,3,4,5], k = 2
输出：[2,1,4,3,5]

image.png

1
2
输入：head = [1,2,3,4,5], k = 3
输出：[3,2,1,4,5]

代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
public ListNode reverseKGroup(ListNode head, int k) {
      if (head == null || k <= 1) {
          return head;
      }

      // 创建一个虚拟头节点，方便处理链表头部的反转
      ListNode dummy = new ListNode(0);
      dummy.next = head;
      ListNode prevGroupEnd = dummy;

      while (true) {
          // 检查是否有足够的节点进行反转
          ListNode kthNode = getKthNode(prevGroupEnd, k);
          if (kthNode == null) {
              break; // 不足 k 个节点，停止反转
          }

          ListNode nextGroupStart = kthNode.next;
          ListNode[] reversedGroup = reverseList(prevGroupEnd.next, k);
          prevGroupEnd.next = reversedGroup[0]; // 连接反转后的子链表
          prevGroupEnd = reversedGroup[1]; // 更新 prevGroupEnd 到当前反转组的末尾

          prevGroupEnd.next = nextGroupStart; // 连接下一组
      }

      return dummy.next;
  }

  // 获取从 start 节点开始的第 k 个节点
  private ListNode getKthNode(ListNode start, int k) {
      while (start != null && --k >= 0) {
          start = start.next;
      }
      return start;
  }

  // 反转从 head 开始的 k 个节点，并返回反转后的头和尾
  private ListNode[] reverseList(ListNode head, int k) {
      ListNode prev = null;
      ListNode cur = head;
      ListNode next = null;
      for (int i = 0; i < k; i++) {
          next = cur.next;
          cur.next = prev;
          prev = cur;
          cur = next;
      }
      return new ListNode[] {prev, head}; // 返回反转后的头和尾
  }

8. 删除链表的倒数第 N 个结点

【链表】、【双指针】

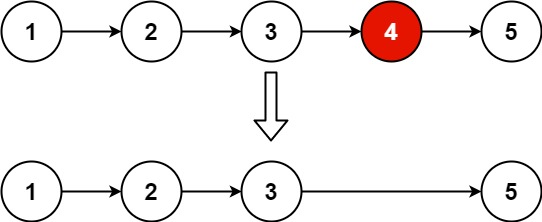
给你一个链表，删除链表的倒数第 n **个结点，并且返回链表的头结点。

**进阶：**你能尝试使用一趟扫描实现吗？

提示：

链表中结点的数目为 sz

1 <= sz <= 30

0 <= Node.val <= 100

1 <= n <= sz

示例：

image.png

1
2
输入：head = [1,2,3,4,5], n = 2
输出：[1,2,3,5]
1
2
输入：head = [1], n = 1
输出：[]
1
2
输入：head = [1,2], n = 1
输出：[1]

代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
public ListNode removeNthFromEnd(ListNode head, int n) {
    ListNode dummy = new ListNode(0, head);
    int length = getLength(head);
    ListNode cur = dummy;
    for (int i = 1; i < length - n + 1; ++i) {
        cur = cur.next;
    }
    cur.next = cur.next.next;
    ListNode ans = dummy.next;
    return ans;
}

public int getLength(ListNode head) {
    int length = 0;
    while (head != null) {
        ++length;
        head = head.next;
    }
    return length;
}

9. 两两交换链表中的节点

给你一个链表，两两交换其中相邻的节点，并返回交换后链表的头节点。你必须在不修改节点内部的值的情况下完成本题（即，只能进行节点交换）。

提示：

链表中节点的数目在范围 [0, 100] 内

0 <= Node.val <= 100

示例：

image.png

1
2
输入：head = [1,2,3,4]
输出：[2,1,4,3]
1
2
输入：head = []
输出：[]
1
2
输入：head = [1]
输出：[1

代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
public ListNode swapPairs(ListNode head) {
     if (head == null || head.next == null) {
         return head;
     }
     ListNode dumpNode1 = new ListNode(0, head);
     ListNode dumpNode = dumpNode1;
     while (dumpNode.next != null && dumpNode.next.next != null) {
         ListNode temp2 = dumpNode.next.next;
         ListNode temp1 = dumpNode.next;
         dumpNode.next = temp2;
         temp1.next = temp2.next;
         temp2.next = temp1;
         dumpNode = temp1;
     }
     return dumpNode1.next;
 }

10. 合并 K 个升序链表

【链表】、【分治】、【堆】、【归并排序】

给你一个链表数组，每个链表都已经按升序排列。

请你将所有链表合并到一个升序链表中，返回合并后的链表。

提示：

k == lists.length

0 <= k <= 10^4

0 <= lists[i].length <= 500

10^4 <= lists[i][j] <= 10^4

lists[i] 按 升序 排列

lists[i].length 的总和不超过 10^4

示例：

1
2
3
4
5
6
7
8
9
10
输入：lists = [[1,4,5],[1,3,4],[2,6]]
输出：[1,1,2,3,4,4,5,6]
解释：链表数组如下：
[
  1->4->5,
  1->3->4,
  2->6
]
将它们合并到一个有序链表中得到。
1->1->2->3->4->4->5->6
1
2
输入：lists = []
输出：[]
1
2
输入：lists = [[]]
输出：[]

代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
public ListNode mergeKLists(ListNode[] lists) {
    if (lists == null || lists.length == 0) {
        return null; // 边界条件：如果链表数组为空，返回 null
    }
    return mergeKListsHelper(lists, 0, lists.length - 1); // 调用分治递归函数
}

private ListNode mergeKListsHelper(ListNode[] lists, int start, int end) {
    if (start == end) {
        return lists[start]; // 如果只剩下一个链表，直接返回
    }
    if (start > end) {
        return null; // 无效区间，返回 null
    }
    int mid = start + (end - start) / 2; // 计算中间索引
    ListNode left = mergeKListsHelper(lists, start, mid); // 递归合并左半部分
    ListNode right = mergeKListsHelper(lists, mid + 1, end); // 递归合并右半部分
    return mergeTwoLists(left, right); // 合并左右两部分
}

private ListNode mergeTwoLists(ListNode l1, ListNode l2) {
    ListNode dummy = new ListNode(0); // 创建虚拟头节点
    ListNode current = dummy;

    while (l1 != null && l2 != null) { // 遍历两个链表
        if (l1.val < l2.val) {
            current.next = l1; // 取较小的节点
            l1 = l1.next;
        } else {
            current.next = l2;
            l2 = l2.next;
        }
        current = current.next; // 移动指针
    }

    if (l1 != null) {
        current.next = l1; // 连接剩余的链表
    } else {
        current.next = l2;
    }

    return dummy.next; // 返回合并后的链表
}

11. 合并两个有序链表

【链表】、【归并排序】

将两个升序链表合并为一个新的 升序 链表并返回。新链表是通过拼接给定的两个链表的所有节点组成的。

提示：

两个链表的节点数目范围是 [0, 50]

100 <= Node.val <= 100

l1 和 l2 均按 非递减顺序 排列

示例：

1
2
输入：l1 = [1,2,4], l2 = [1,3,4]
输出：[1,1,2,3,4,4]

代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
/**
 * Definition for singly-linked list.
 * public class ListNode {
 *     int val;
 *     ListNode next;
 *     ListNode() {}
 *     ListNode(int val) { this.val = val; }
 *     ListNode(int val, ListNode next) { this.val = val; this.next = next; }
 * }
 */
class Solution {
    public ListNode mergeTwoLists(ListNode l1, ListNode l2) {
        if (l1 == null) {
            return l2;
        } else if (l2 == null) {
            return l1;
        } else if (l1.val < l2.val) {
            l1.next = mergeTwoLists(l1.next, l2);
            return l1;
        } else {
            l2.next = mergeTwoLists(l1, l2.next);
            return l2;
        }
    }
}

12. 随机链表的复制

【哈希表】、【链表】

给你一个长度为 n 的链表，每个节点包含一个额外增加的随机指针 random ，该指针可以指向链表中的任何节点或空节点。

构造这个链表的 深拷贝。 深拷贝应该正好由 n 个 全新 节点组成，其中每个新节点的值都设为其对应的原节点的值。新节点的 next 指针和 random 指针也都应指向复制链表中的新节点，并使原链表和复制链表中的这些指针能够表示相同的链表状态。复制链表中的指针都不应指向原链表中的节点 。

例如，如果原链表中有 X 和 Y 两个节点，其中 X.random --> Y 。那么在复制链表中对应的两个节点 x 和 y ，同样有 x.random --> y 。

返回复制链表的头节点。

用一个由 n 个节点组成的链表来表示输入/输出中的链表。每个节点用一个 [val, random_index] 表示：

  • val：一个表示 Node.val 的整数。
  • random_index：随机指针指向的节点索引（范围从 0 到 n-1）；如果不指向任何节点，则为 null 。

你的代码 只 接受原链表的头节点 head 作为传入参数。

提示：

0 <= n <= 1000

104 <= Node.val <= 104

Node.random 为 null 或指向链表中的节点。

示例：

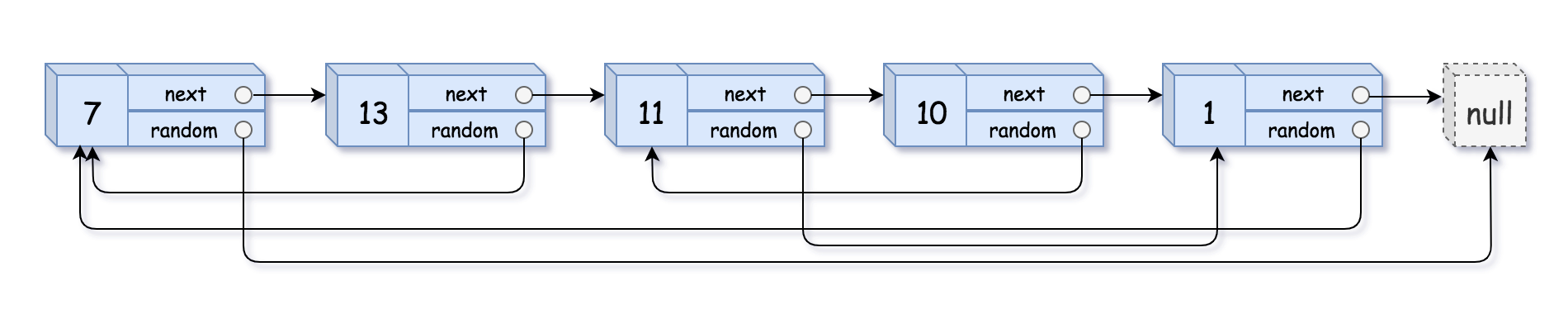
image.png

1
2
输入：head = [[7,null],[13,0],[11,4],[10,2],[1,0]]
输出：[[7,null],[13,0],[11,4],[10,2],[1,0]]

image.png

1
2
输入：head = [[1,1],[2,1]]
输出：[[1,1],[2,1]]

image.png

1
2
输入：head = [[3,null],[3,0],[3,null]]
输出：[[3,null],[3,0],[3,null]]

代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
/**
 * 复制带有随机指针的链表
 * <p>
 * 本方法通过三步完成复制： 1. 在原链表中每个节点后复制一个新节点 2. 设置新节点的随机指针 3. 将原链表和复制的新链表分离
 *
 * @param head 原链表的头节点
 * @return 复制后的新链表的头节点
 */
public Node copyRandomList(Node head) {
    if (head == null) {
        return null;
    }
    
    // 第一步：复制每个节点，并插入到原节点后面
    Node current = head;
    while (current != null) {
        Node newNode = new Node(current.val);
        newNode.next = current.next;
        current.next = newNode;
        current = newNode.next;
    }
    
    // 第二步：设置随机指针
    current = head;
    while (current != null) {
        if (current.random != null) {
            current.next.random = current.random.next;
        }
        current = current.next.next;
    }
    
    // 第三步：分离两个链表
    current = head;
    Node newHead = head.next;
    Node newCurrent = newHead;
    while (newCurrent.next != null) {
        current.next = current.next.next;
        newCurrent.next = newCurrent.next.next;
        current = current.next;
        newCurrent = newCurrent.next;
    }
    current.next = null;
    
    return newHead;
}

13. 排序链表

【链表】、【双指针】、【分治】、【排序】、【归并排序】

给你链表的头结点 head ，请将其按 升序 排列并返回 排序后的链表 。

**进阶：**你可以在 O(n log n) 时间复杂度和常数级空间复杂度下，对链表进行排序吗？

提示：

链表中节点的数目在范围 [0, 5 * 104] 内

105 <= Node.val <= 105

示例：

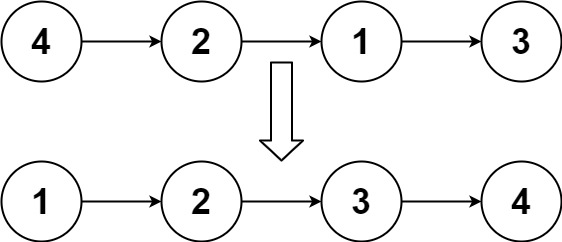
image.png

1
2
输入：head = [4,2,1,3]
输出：[1,2,3,4]

代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
public ListNode sortList(ListNode head) {
    if (head == null || head.next == null) {
        return head;
    }

    // 找到链表的中间节点
    ListNode mid = findMiddle(head);
    ListNode rightHead = mid.next;
    mid.next = null;

    // 递归地对左右两部分进行排序
    ListNode left = sortList(head);
    ListNode right = sortList(rightHead);

    // 合并两个有序链表
    return merge(left, right);
}

private ListNode findMiddle(ListNode head) {
    ListNode slow = head, fast = head;
    while (fast != null && fast.next != null) {
        fast = fast.next.next;
        if (fast == null || fast.next == null) {
            break;
        }
        slow = slow.next;
    }
    return slow;
}

private ListNode merge(ListNode l1, ListNode l2) {
    ListNode dummy = new ListNode(0);
    ListNode cur = dummy;
    while (l1 != null && l2 != null) {
        if (l1.val < l2.val) {
            cur.next = l1;
            l1 = l1.next;
        } else {
            cur.next = l2;
            l2 = l2.next;
        }
        cur = cur.next;
    }
    cur.next = l1 != null ? l1 : l2;
    return dummy.next;
}

14. LRU缓存

请你设计并实现一个满足  LRU (最近最少使用) 缓存 约束的数据结构。

实现 LRUCache 类：

  • LRUCache(int capacity) 以 正整数 作为容量 capacity 初始化 LRU 缓存
  • int get(int key) 如果关键字 key 存在于缓存中，则返回关键字的值，否则返回 1 。
  • void put(int key, int value) 如果关键字 key 已经存在，则变更其数据值 value ；如果不存在，则向缓存中插入该组 key-value 。如果插入操作导致关键字数量超过 capacity ，则应该 逐出 最久未使用的关键字。

函数 get 和 put 必须以 O(1) 的平均时间复杂度运行。

提示：

1 <= capacity <= 3000

0 <= key <= 10000

0 <= value <= 105

最多调用 2 * 105 次 get 和 put

示例：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
输入
["LRUCache", "put", "put", "get", "put", "get", "put", "get", "get", "get"]
[[2], [1, 1], [2, 2], [1], [3, 3], [2], [4, 4], [1], [3], [4]]
输出
[null, null, null, 1, null, -1, null, -1, 3, 4]

解释
LRUCache lRUCache = new LRUCache(2);
lRUCache.put(1, 1); // 缓存是 {1=1}
lRUCache.put(2, 2); // 缓存是 {1=1, 2=2}
lRUCache.get(1);    // 返回 1
lRUCache.put(3, 3); // 该操作会使得关键字 2 作废，缓存是 {1=1, 3=3}
lRUCache.get(2);    // 返回 -1 (未找到)
lRUCache.put(4, 4); // 该操作会使得关键字 1 作废，缓存是 {4=4, 3=3}
lRUCache.get(1);    // 返回 -1 (未找到)
lRUCache.get(3);    // 返回 3
lRUCache.get(4);    // 返回 4

代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
public class LRUCache {
    class DLinkedNode {
        int key;
        int value;
        DLinkedNode prev;
        DLinkedNode next;
        public DLinkedNode() {}
        public DLinkedNode(int _key, int _value) {key = _key; value = _value;}
    }

    private Map<Integer, DLinkedNode> cache = new HashMap<Integer, DLinkedNode>();
    private int size;
    private int capacity;
    private DLinkedNode head, tail;

    public LRUCache(int capacity) {
        this.size = 0;
        this.capacity = capacity;
        // 使用伪头部和伪尾部节点
        head = new DLinkedNode();
        tail = new DLinkedNode();
        head.next = tail;
        tail.prev = head;
    }

    public int get(int key) {
        DLinkedNode node = cache.get(key);
        if (node == null) {
            return -1;
        }
        // 如果 key 存在，先通过哈希表定位，再移到头部
        moveToHead(node);
        return node.value;
    }

    public void put(int key, int value) {
        DLinkedNode node = cache.get(key);
        if (node == null) {
            // 如果 key 不存在，创建一个新的节点
            DLinkedNode newNode = new DLinkedNode(key, value);
            // 添加进哈希表
            cache.put(key, newNode);
            // 添加至双向链表的头部
            addToHead(newNode);
            ++size;
            if (size > capacity) {
                // 如果超出容量，删除双向链表的尾部节点
                DLinkedNode tail = removeTail();
                // 删除哈希表中对应的项
                cache.remove(tail.key);
                --size;
            }
        }
        else {
            // 如果 key 存在，先通过哈希表定位，再修改 value，并移到头部
            node.value = value;
            moveToHead(node);
        }
    }

    private void addToHead(DLinkedNode node) {
        node.prev = head;
        node.next = head.next;
        head.next.prev = node;
        head.next = node;
    }

    private void removeNode(DLinkedNode node) {
        node.prev.next = node.next;
        node.next.prev = node.prev;
    }

    private void moveToHead(DLinkedNode node) {
        removeNode(node);
        addToHead(node);
    }

    private DLinkedNode removeTail() {
        DLinkedNode res = tail.prev;
        removeNode(res);
        return res;
    }
}